强化学习PPO

Policy Gradient

basic

每一个eposide记录为$\tau$

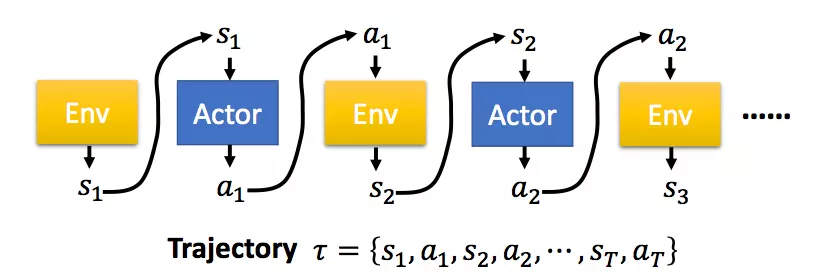
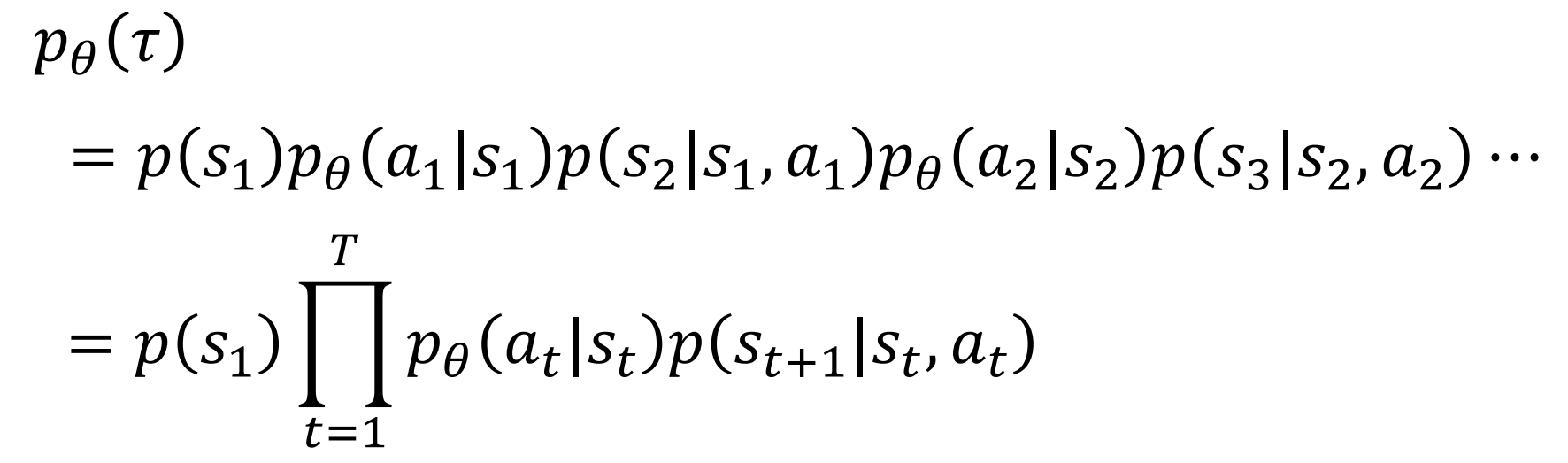
$p_\theta(\tau)$是按策略参数为$\theta$得到这样一个trajectory的概率

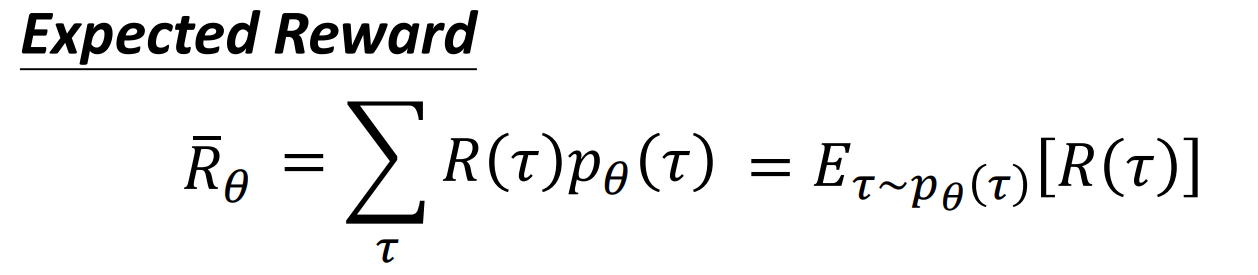
要提高这个期望，使用梯度上升，对$\theta$求梯度使用上式中的中间这个求和形式，使用技巧

$\bigtriangledown f(x) = f(x)\bigtriangledown \log{f(x)}$

这样可以转化为概率采样的形式，

$\begin{aligned} \bigtriangledown\overline{R_\theta} & =\bigtriangledown\sum_{\tau}{R(\tau)p_\theta(\tau)} \\& = \sum_\tau{R(\tau)p_\theta(\tau)\bigtriangledown \log{p_\theta(\tau)}} \\& = E_{\tau\sim p_\theta}(R(\tau)\bigtriangledown{\log{p_\theta(\tau)}}) \\& \approx \frac{1}{N}\sum_{n=1}^N{R(\tau^n)\bigtriangledown{\log{p_\theta(\tau^n)}}} \\& = \frac{1}{N}\sum_{n=1}^{N}\sum_{t=1}^{T_n}R(\tau^n)\bigtriangledown{\log{p_\theta (a_t^n|s_t^n)}} \end{aligned}$

最后一行中因为我们的梯度不关心$p(s_{t+1}|s_t,a_t)$所以直接忽略掉，$R(\tau^n)$应该放在积分号中间也可以。

我们可以看到这个梯度与$\theta$有关，所以每次更新梯度，都需要重新采样N次，也就是需要与环境交互，跑一个$\tau$出来，然后更新梯度，然后就需要重新再交互，这相当于是on-policy，换成off-policy就是PPO。

进行ppo之前先有两个tips。

tip 1: add a base line

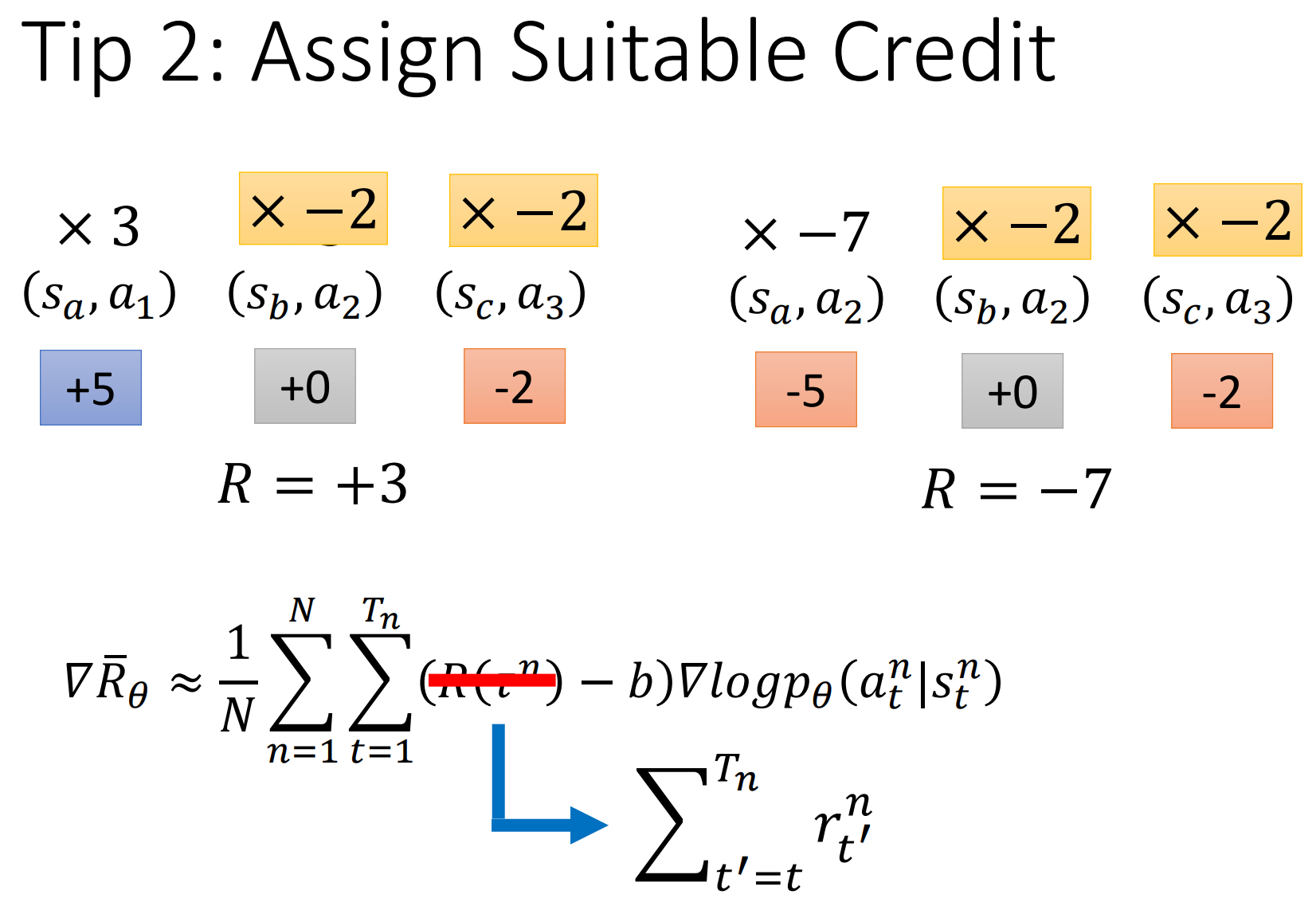
PG方法在更新策略时，基本思想就是增加reward大的动作出现的概率，减小reward小的策略出现的概率。假设现在有一种情况，我们的reward在无论何时都是正的，对于没有采样到的动作，它的reward是0。因此，如果一个比较好的动作没有被采样到，而采样到的不好的动作得到了一个比较小的正reward，那么没有被采样到的好动作的出现概率会越来越小，这显然是不合适的，因此我们需要增加一个奖励的基线，让reward有正有负。增加的基线是所获得奖励的平均值b。

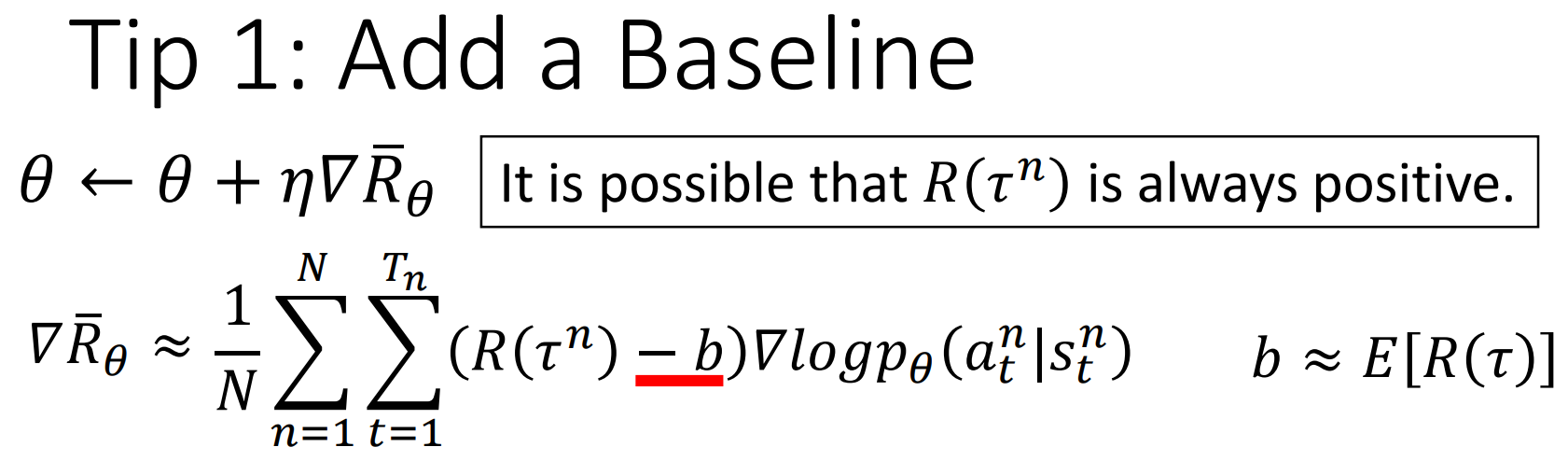
tip 2: Assign Suitable Credit

当前动作之后获得的奖励才重要

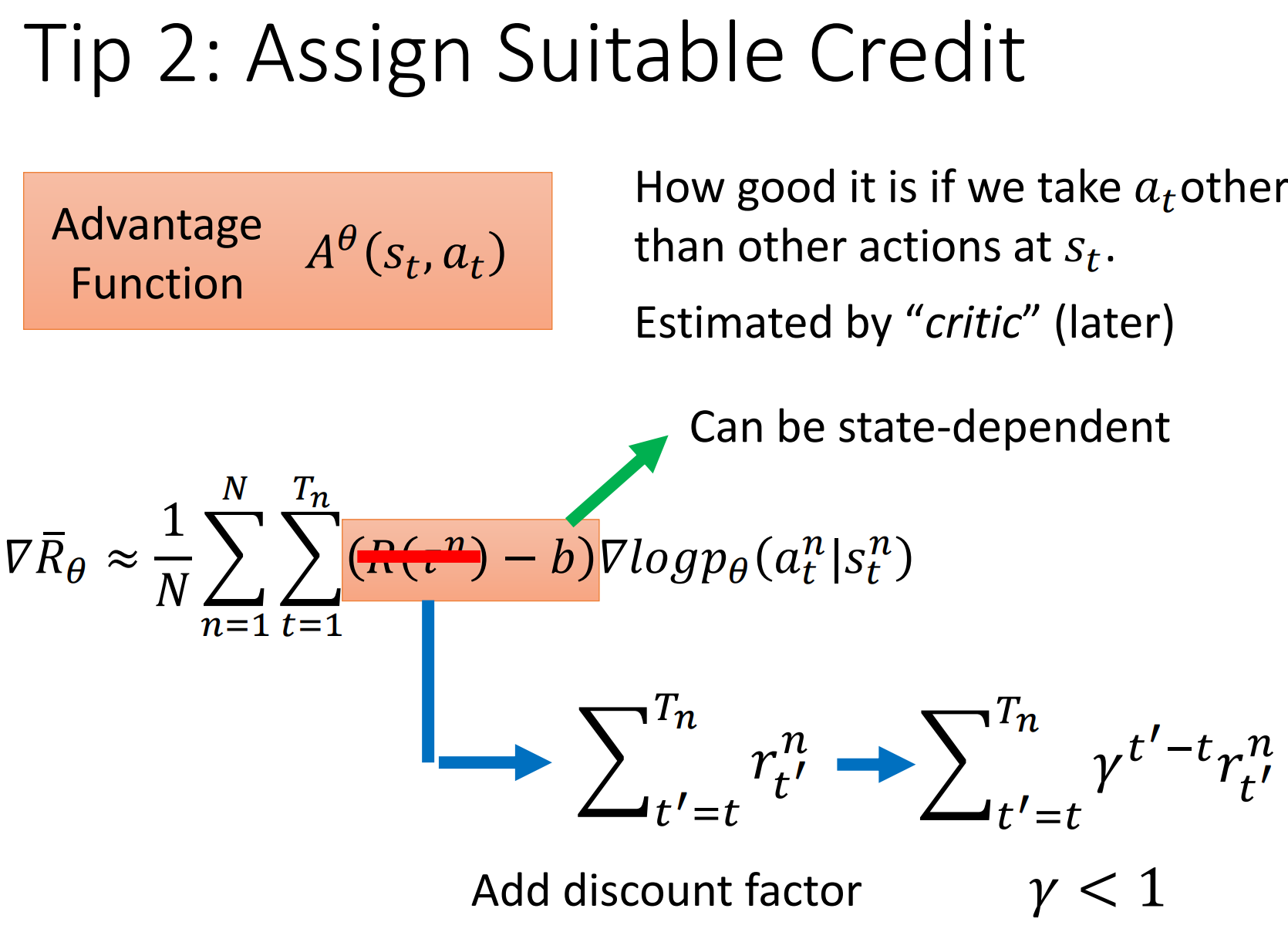
添加一个discount，前面那个系数可以用Advantage Function表示：$A^\theta(s_t,a_t)$

这个相当于在时间t之后得到的价值总和（忘了专业名词叫啥了）

Proximal Policy Optimization

采用重要性采样

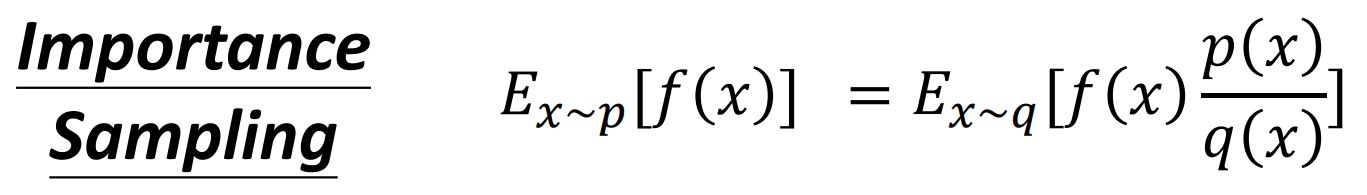
可以从p的分布采样，换到从q的分布采样，需要注意，p和q的分布差异不能太大，因为虽然上式的均值相同，但是方差不同，还是会有影响。

$\bigtriangledown\overline{R_\theta}= \frac{1}{N}\sum_{n=1}^{N}\sum_{t=1}^{T_n}R(\tau^n)\bigtriangledown{\log{p_\theta (a_t^n|s_t^n)}}$

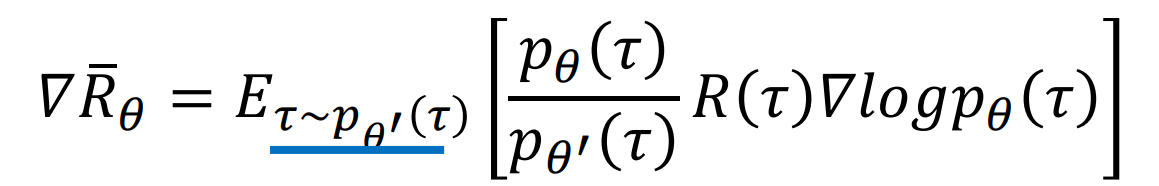
这里为什么是从$\pi_\theta$中sample出$(s_t,a_t)$怪不清楚的，现在的理解是

我们需要控制$\theta$和$\theta’$相似，使用KL divergence，这里肯定比较的是$p\theta(\bullet|s)$和$p{\theta’}(\bullet|s)$的距离

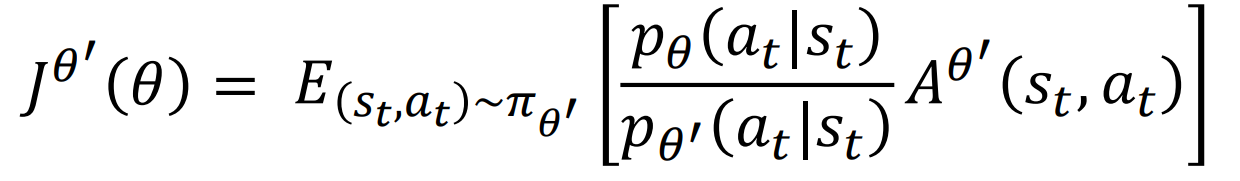
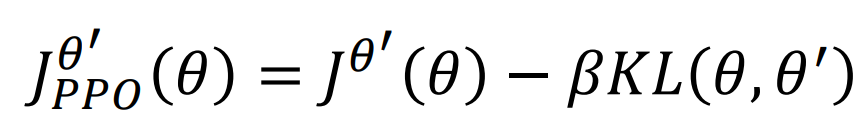
算法流程：

Initial policy parameters $\theta^0$
In each iteration
- Using $\theta^k$ to interact with the environment to collect $s_t,a_t$ and compute advantage $A^{\theta^k}(s_t,a_t)$
- Find $\theta$ optimizeing $J^{\theta^k}(\theta)-\beta KL(\theta,\theta^k)$

上面这些来自于李宏毅课程.pdf) 。

有几点没有懂

新的策略需要凑一条条完整的流程$\tau$吗
advantage function 应该怎么计算
为什么要优化函数J

更正：

重新看了下课程，之前弄错了，$\theta’$才是与环境交互的:smile:

优化的J的原因是，$\bigtriangledown f(x) = f(x)\bigtriangledown \log{f(x)}$相当于原函数是f(x)，也就是这里的J

在算kl divergence的时候，把所有sample到的$s_t$都算下两个model的输出的区别，这个好像还比较麻烦，具体怎么处理还不清楚

TRPO

简单写下PPO的前身，更麻烦的处理方式，TRPO讲KL divergence项作为一个constrain，不在optimize项里面。

PPO2

PPO2 提出了不用计算KL Divergence的方法

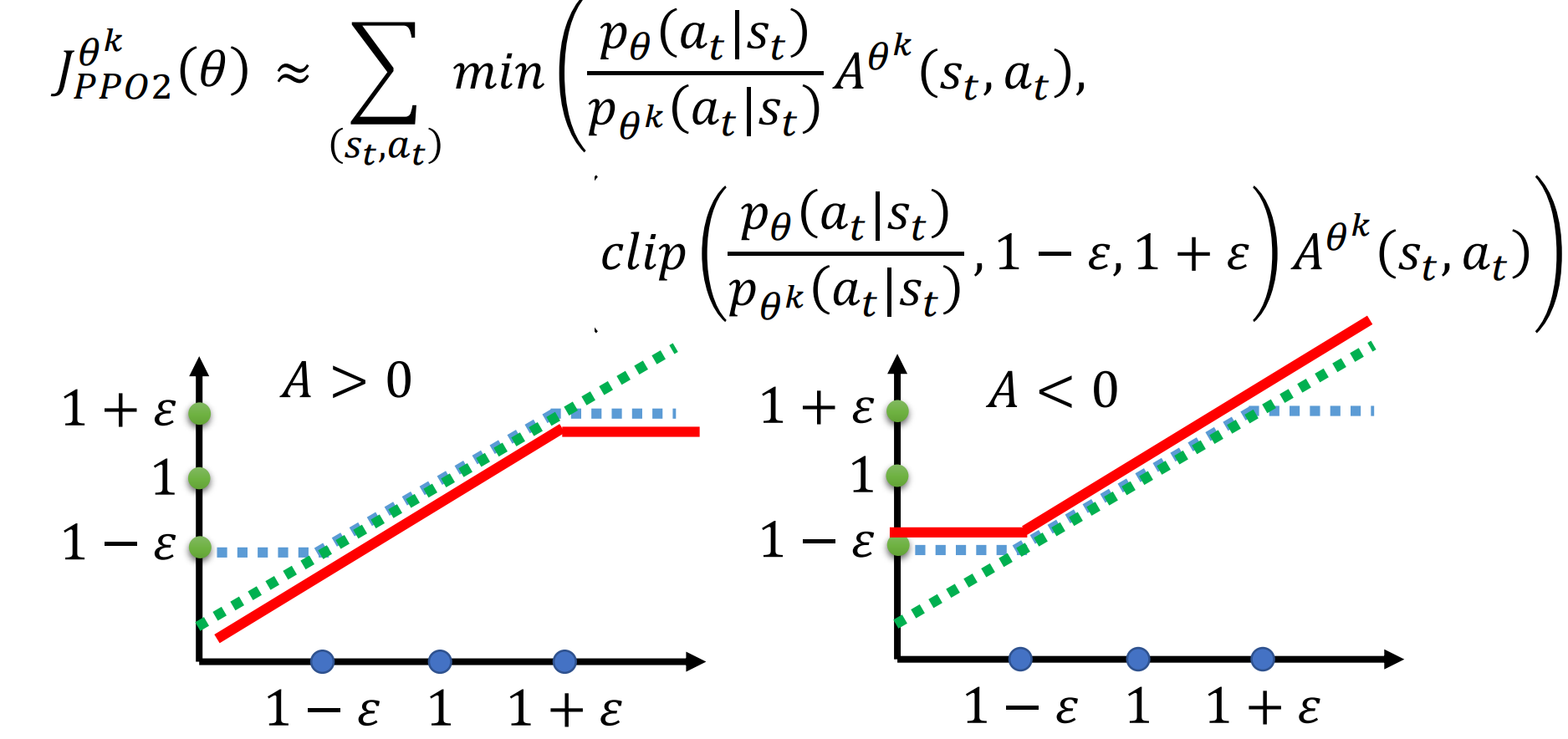
clip的意思是如果$p\theta$和$p{\theta’}$ 的比值如果小于$1-\varepsilon$则等于$1-\varepsilon$。

图中横轴是clip里的第一项纵轴是输出结果。

具体算法流程：

可以看到在训练过程中，是需要再学一个value function去估测advantage的。