Ch1.1-Ch1.6：崔昊川
https://blog.csdn.net/qq_41608822/article/details/105902504
Ch2.1-Ch2.4：韦国梁
见正文
Ch2.5-Ch2.8：崔昊川
https://blog.csdn.net/qq_41608822/article/details/105928928
Ch3.1-Ch3.3：韦国梁
见正文
Ch3.4-Ch3.8：崔昊川
https://blog.csdn.net/qq_41608822/article/details/106187983
Ch4.1-Ch4.5：韦国梁
见正文
Ch4.6-Ch5.2：崔昊川
https://blog.csdn.net/qq_41608822/article/details/106289904
Ch5.3-Ch5.7：韦国梁
见正文
Ch5.8-Ch6.3：崔昊川
https://blog.csdn.net/qq_41608822/article/details/106468105
2.1 A k-Armed Bandit Problem
在k-手臂匪徒问题中， 你每次面临k个不同选项或操作中的选择。 在每次选择后，你会收到一个数值奖励，该数值奖励取决于您选择的行动的平稳概率分布。 你的目标是最大化某段时间内的预期总回报，例如，超过1000个动作选择或时间步骤。
在我们的k-手臂匪徒问题中，考虑到该行动被选中，k个行动中的每一个行动都具有预期的或平均的奖励; 现在让我们将其称之为该行动的价值。 我们表示在时间步骤 t 选择的行动为 At ，相应的回报为 Rt 。 q∗(a)表示为任意行为的值是 a的时候， 选择时的期望回报：
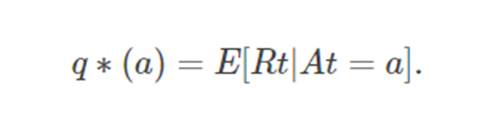
如果我们知道每个action对应的value，那么我们只需要每次都选择最高的那个value对应的action即可，但事实却是我们在玩游戏之前，不知道每个action确切的value，我们可以通过多次测试来估计每个action的value,将t 时刻的action a对应的估计价值（estimated value) 记作 Qt(a) ,我们的目标是使得 Qt(a)尽可能的接近q∗(a),然后根据Qt(a)选择 a.
2.2 Action-Value Methods
最简单的value 估计方式就是sample-average（采样平均），即
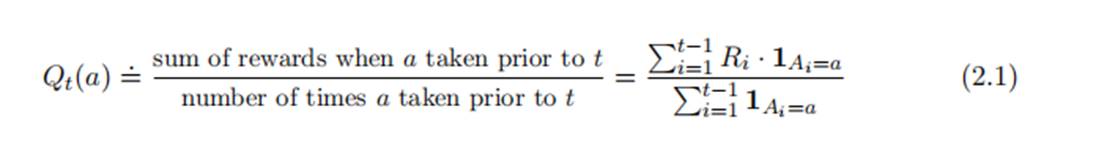其中，
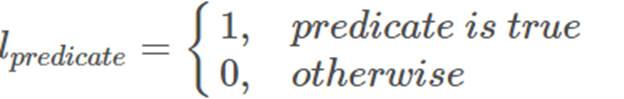
简单来说就是对每个action a对应的奖励做平均。通过增加实验次数，当实验次数趋于无穷大时，Qt(a) 趋于 q∗(a)
greedy 与 ϵ-greedy
greedy方法：
如果我们每次都选择最大value对应的action，即
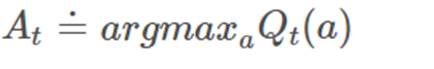
那么我们采取的是greedy policy。
ϵ-greedy：
如果我们会在一些时间内选择最大value对应action外的其他action，则表明我们对环境进行了Exploration。ϵ-greedy方法在greedy方法基础上进行改进：
2.3 The 10-armed Testbed
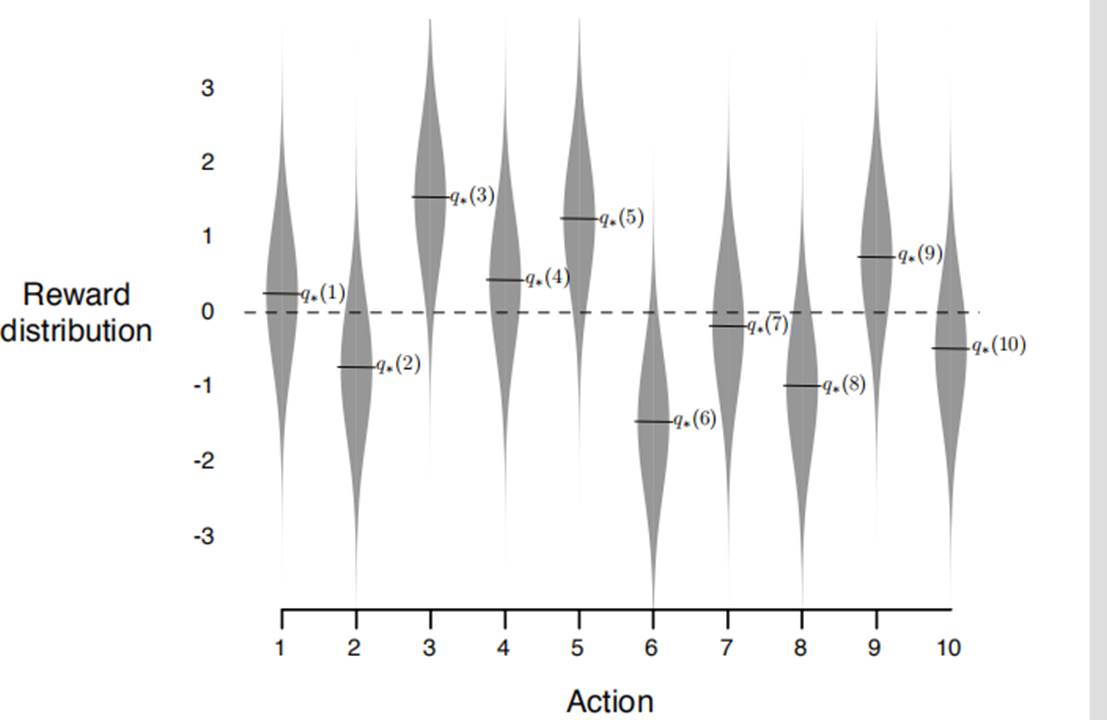
要评测强化学习的优劣，需要一个模型，the 10-arm testbed就是其中一个，可以一次在2000组上进行评测，在每一组中，每一组有一个独立的模型，每一次选择a对应的reward是通过q*(a)的一个高斯分布来返回的，然后再所有组上的表现可以代表我们算法的平均行为。
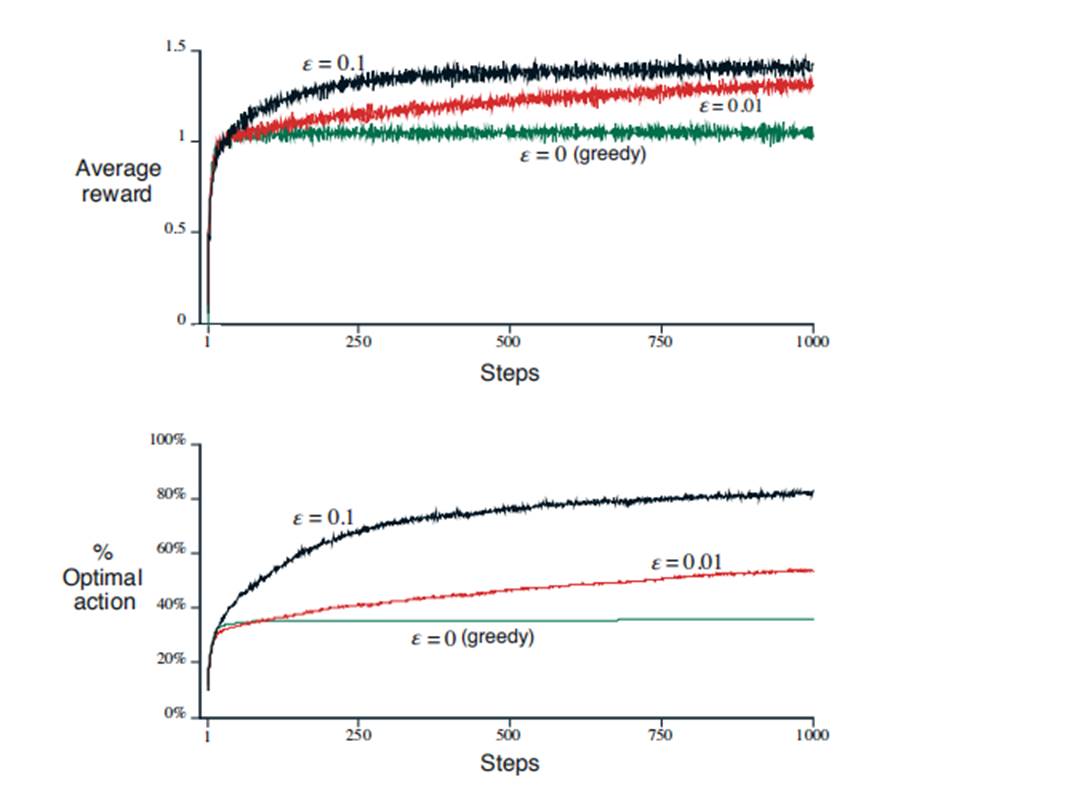
上图简单来说代表了greedy和ϵ-greedy的优劣。通常来说，两种方法都会随着探索次数增加，效果越来越好。Greedy方法可能刚开始比其他更快，但是长远来看，由于短时，不探索的原因，最后效果不如ϵ-greedy。
通常来说，如果任务方差小，greedy表现更好，反之ϵ-greedy表现更好。所以在实际中，两种方法需要在exploration 和exploitation之间找到平衡。
2.4 Incremental Implementation
上一节介绍的sample average方法是将所有的历史信息全部记录下来然后求平均，如果历史记忆很长，甚至无限，那么直接求解将受到内存和运行时间的限制。下面将结合数学中的迭代思想推导出增量式的求解方法，该方法仅耗费固定大小的内存，且可以单步更新。
为了简化表达，我们只关注一个action,假设Ri是第 i 次选择这个action所获得的reward， 将这个action第n 次被选择的estimate value表示为Qn+1，
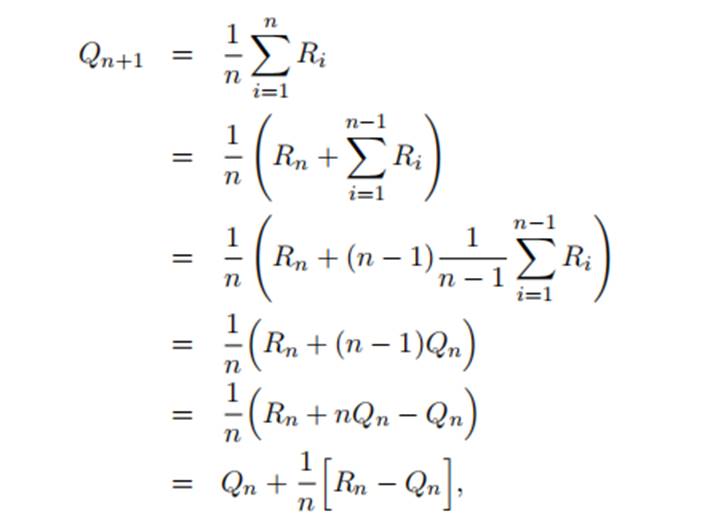
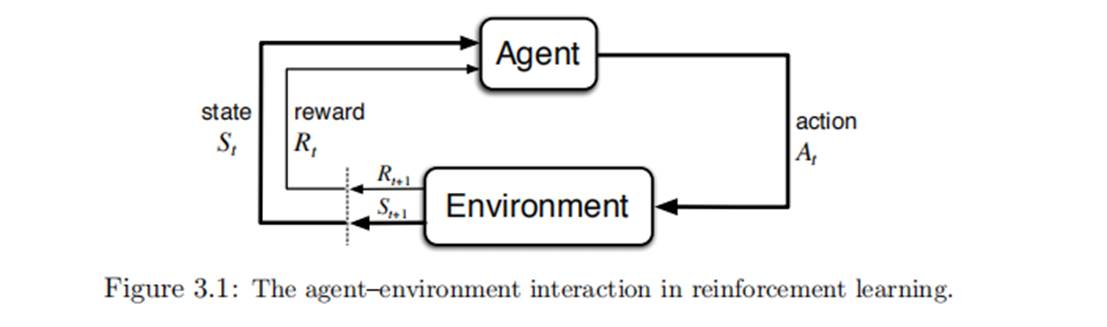
3.1 “智能体-环境”交互接口
有限马尔可夫决策过程MDP是一种通过交互式学习来实现目标的理论框架，包含以下元素：
智体：实施决策的机器
环境: 智体之外所有与其相互作用的事务
收益：智体选择交互后，环境会呈现新的状态，并且产生收益，智体的目标是最大化累计收益。
有限马尔可夫性：
St和Rt的每个可能的值出现的概率只取决于前一个状态St-1和前一个动作At-1，并且与更早之前的状态和动作无关。
基于以上特性，可以推出以下四个公式：
随机变量Rt和St的概率分布：
P（s’,r|s,a）=Pr{St=s’,Rt=r|St-1=s,At-1=a}
状态转移概率：
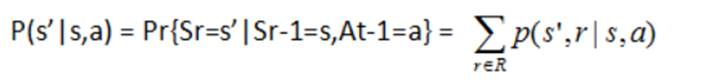
状态-动作 二元组的期望收益：
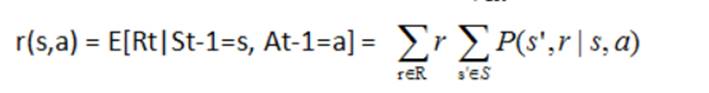
状态-动作-后继状态 三元组的期望收益：
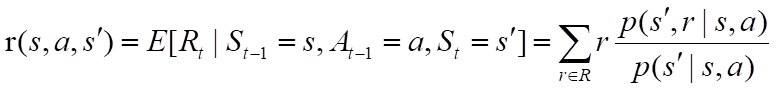
3.2 目标和收益
在强化学习中，智能体的目标被形式化表征为一种特殊的信号，称为收益，通过环境传递给智能体。
我们所有的目标都可以归结为：最大化智能体接收到的标量信号（收益）累积和的概率期望值。
一般的，我们将目标设定为取得最大收益时的情况，不可以将收益设定为完成目标的先验知识。举例：在国际象棋中，如果设定吃子为收益，而不是达成胜利，智能体可能为了尽可能多的吃子，达成最大收益而输掉比赛。
3.3 回报和分幕
在有终止情况的任务下，比如下棋，智能体和环境交互可以被自然的分成一系列子系列，每个包含终止情况的子系列称为幕。
对于分慕情况，优化目标为：
Gt=Rt+1 + Rt+2 + Rt+3 + Rt+4 +…+RT
T为终止时刻
而对于无法分幕的连续过程，优化目标调整为：
Gt=Rt+1 + yRt+2 +y^2Rt+3+…
Gt=Rt+1+yGt+1
其中
0<=y<=1
y称为折扣率，引入折扣率是防止G趋于无穷大。折扣率决定了未来收益的现值：未来时刻k的收益率只有它的当前值的y^（k-1）倍。y越小，智能体越关注当前收益，y越大，智能体相对越有远见，关注未来收益/
本章节主要介绍了基于动态规划来求解最优策略。
4.1策略评估
对于策略Π，其状态价值函数定义如下：
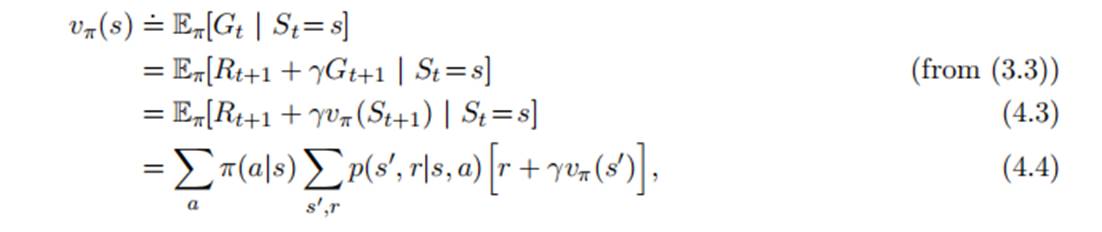
其中，Π（a|s）代表策略，即状态s情况下，选取行动a的概率，由智能体决定。
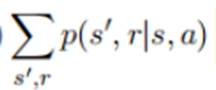为转移概率，是系统的动态特性。
理论上，知道了系统的动态特性和用户的策略，则基于上述公式，仅有状态价值函数为未知数，而对s个状态，有s个等式，可以直接求解，但是由于计算繁琐，采用迭代法求解。
其中，初始化时，除了终止状态的价值函数为0，其余均可以是随机数，采用以下式子迭代：
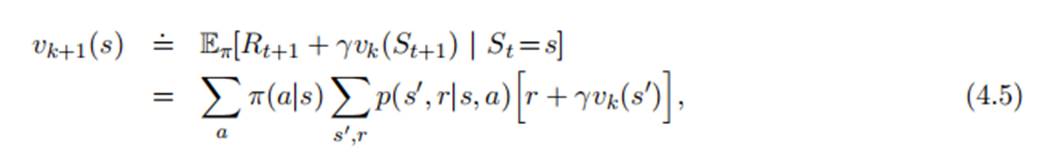
理论上k趋于无穷，终会收敛，但是我们可以在变化很小的时候就停止计算。计算流程如下：
4.2策略改进
知道了给定策略下的价值函数，则可以对策略进行改进。
考虑一种情况，在s状态下，选择新的策略，其余状态下保持策略Π不变，则此动作的价值函数为，
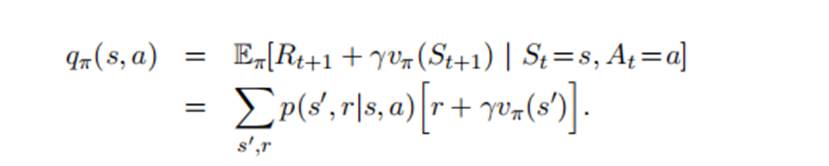
由于其余状态下的策略都一样，要评判策略Π’是否优于策略Π，关键在于判断
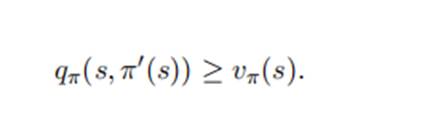
如果上式成立，则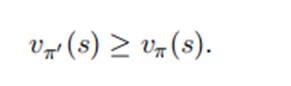
证明如下：
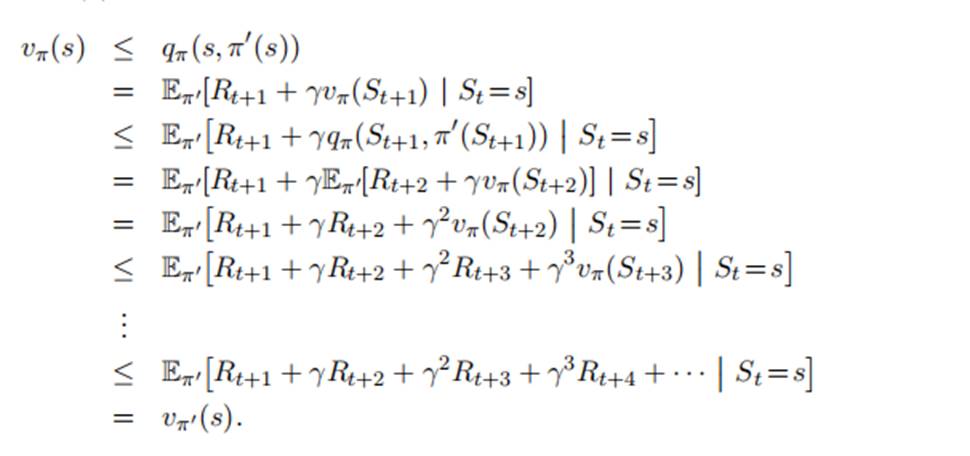
所以证明了，一个策略，如果在一个状态下的动作优于另一个状态下的动作，其余 状态下动作相同，则此策略优于后者策略。由此我们可以使用一种贪心法来求解最优策略，在每个状态选取价值函数最高的动作，不断更新策略。由于动作空间有限，必然可以找到最优策略。
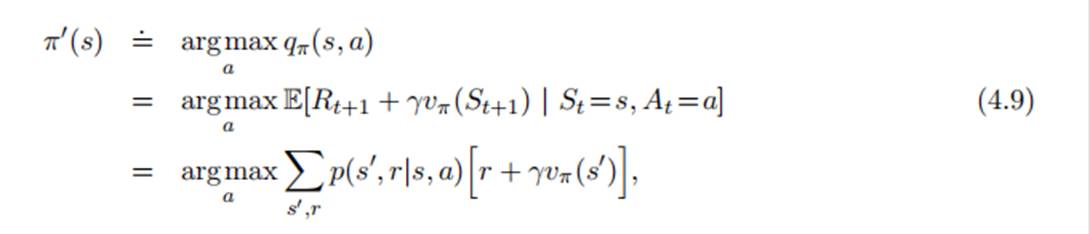
4.3策略迭代
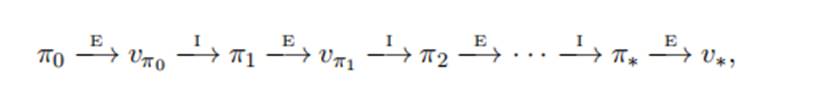
在每个策略中，使用策略评估，计算当前策略的价值函数，然后通过策略改进，得到一个更优的策略，在新的策略中，又需要使用策略评估来收敛，依次循环。
由于一个有限MDP必然只有有限种策略，所以在有限次策略迭代中，必然收敛到最有策略。
流程如下图：
4.4价值迭代
策略迭代的一个缺点是，每次迭代都要使用策略评估，策略评估的收敛非常耗时，可不可以不等策略vΠ收敛就进行策略改进呢？一种特例是，每次评估，只对每个状态更新一次，这种更新方式叫价值迭代。公式如下：
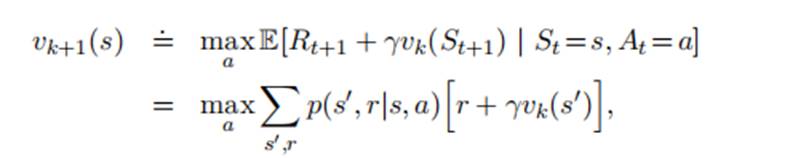
4.5异步动态规划
之前的DP的一大缺点在于，它涉及到对整个状态集的操作，也就是说，他需要对整个状态集进行遍历，如果状态集合很大，哪怕单次遍历，开销也是无法承受的。
异步DP算法是一种就地迭代的算法，随机选择状态值就行更新，可能一个状态值被更新一次，另外一些已经被更新多次。但只要保证，某个时间点，所有状态值都被更新，它终会收敛。
一种典型的异步更新是，在价值迭代的基础上，每次只更新一个状态sk的值，而不是遍历状态集合。
5.3蒙特卡洛控制
采用蒙特卡洛解决控制问题，采用类似于DP算法中广义策略迭代的方式。
在策略迭代中，同时维护近似的策略和近似的价值函数，通过不断迭代逼近真实的价值函数，并且根据价值函数调优策略。
在蒙特卡洛控制中：
策略评估：采用与DP中完全相同的方法，只要每个状态动作都被经历了无数次，蒙特卡洛算法可以收敛到qΠk。
策略改进：采用贪心算法，每次选择当前状态下最大的动作价值函数。可证明总会找到最优策略。
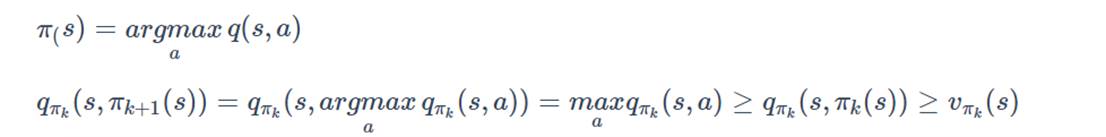
蒙特卡洛控制流程如下:
5.4没有试探性出发假设的蒙特卡洛控制
试探性出发假设:
为了保证每个动作状态都被多次访问，初始化的时候选择不同的状态动作。而这在现实中比较难以满足。
为了解决此问题，提出两种方式。
同轨策略：
用于生成采样数据序列的策略和用于实际决策的待评估和改进的策略是相同的。
离轨策略：
用于生成采样数据序列的策略和用于实际决策的待评估和改进的策略是不同的。
在同轨策略中，策略是软性的，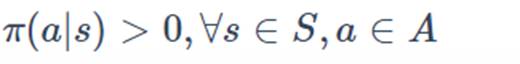
确保每一个动作都被遍历到。为了达到这个目的，采用E-贪心策略。
算法流程如下：
5.5基于重要度采样的离轨策略
离轨策略采用两个策略，一个用来生成样本，更有试探性，称为行动策略。一个用来生成最优策略，称为目标策略。
行为策略必须是完全已知的，并且能被目标策略覆盖。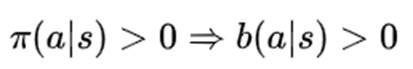
即目标策略所有可能采取到的行动，在行为策略中被选取的概率也必须大于0。
重要度采样：
重要度采样时统计学中估计某一分布性质时使用的一种方法，允许对与原分布中不同的另一个分布采样，再对原分布进行估计。
对于一个 episode ，其子序列的概率为
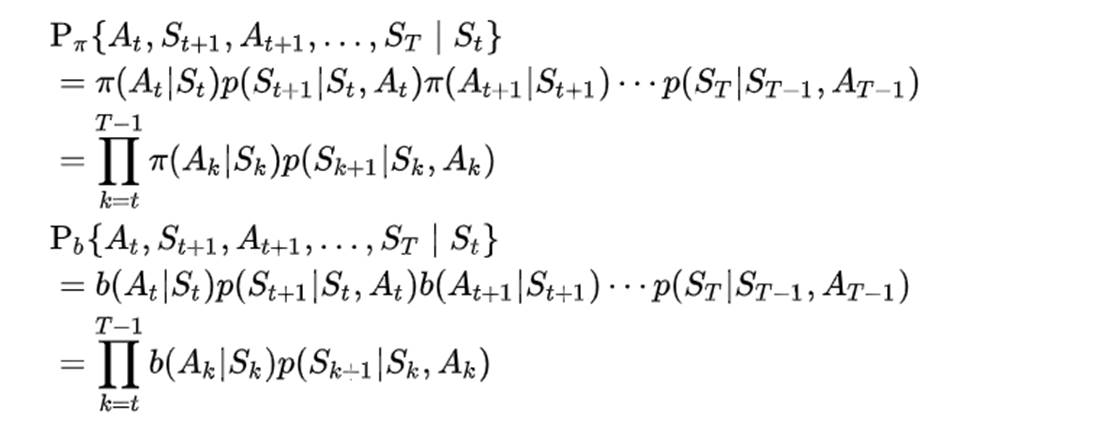
计算出重要性采样比例：
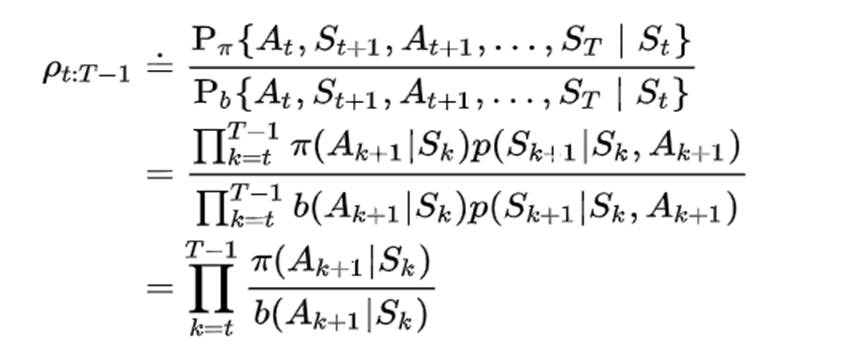
推出
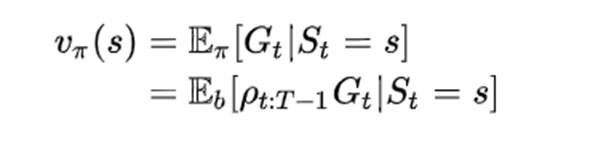
两种估计方法：
5.6增量式实现
与之前的增量更新类似，为了减少记录量，可以使用增量式更新来实现更新。
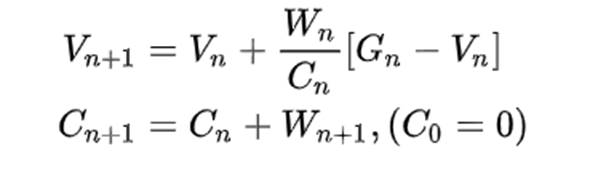
5.7离轨策略蒙特卡洛控制
控制流程如下:
其中目标策略采用固定策略，b策略采用soft策略。
同时W的更新由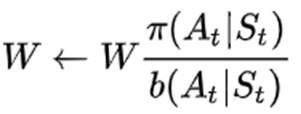
变为
，因为策略是确定的，所以每个状态下采取的动作是确定的。因而