Fairness Is Not Static
Motivation:
当前的Fairness都是静态的，数据都是fixed，而长期动态的环境中，现有的公平算法可能并不适用。
主要内容：
主要介绍了三个 ml-fairness-gym 的仿真环境，通过实验与静态的方法对比，发现静态方法在动态环境中可能会有一些问题。
环境介绍
场景一：Lending
银行设定阈值来作为是否借款的依据，探究不同的策略带来的长期影响和对不同群体的公平影响。
Environment：借款申请人
两个群体，一个优势，一个劣势。
可观测群体属性，离散的信用评分$C\in1,2,3,..,C_{max}$，假定评分到还款概率$\pi(C)$的映射是固定的，优势群体信用评分的分布要高点。
成功还款的话，用户信用上涨c+，agent收益上升r+，如果拖欠，信用下降c-，agent收益下降c-。
Metrics：信用分布，累计的借贷，总真阳率
agent：银行，根据信用评分决定是否借款。
两种agent：
max-reward
寻找阈值最大收益。
因为收益的r+和r-都是定值，所以只要期望大于0应该就可以借，$\pi(C)>\tau$。所以阈值是fixed的。
前200轮全都借，然后找到固定的阈值。
EO
对不同的群体使用不同的阈值，在每一步中，在不同群体TPR相同的限制下最大化收益。用随机插值将ROC补成连续。（ROC如何得到是个问题）
还有很多细节还是得看代码里怎么写的
实验结果
实验是简化的，EO agent是知道当前信用分布的和对应的概率的，那么阈值-真阳率的图像就好做了
初始分布如下：
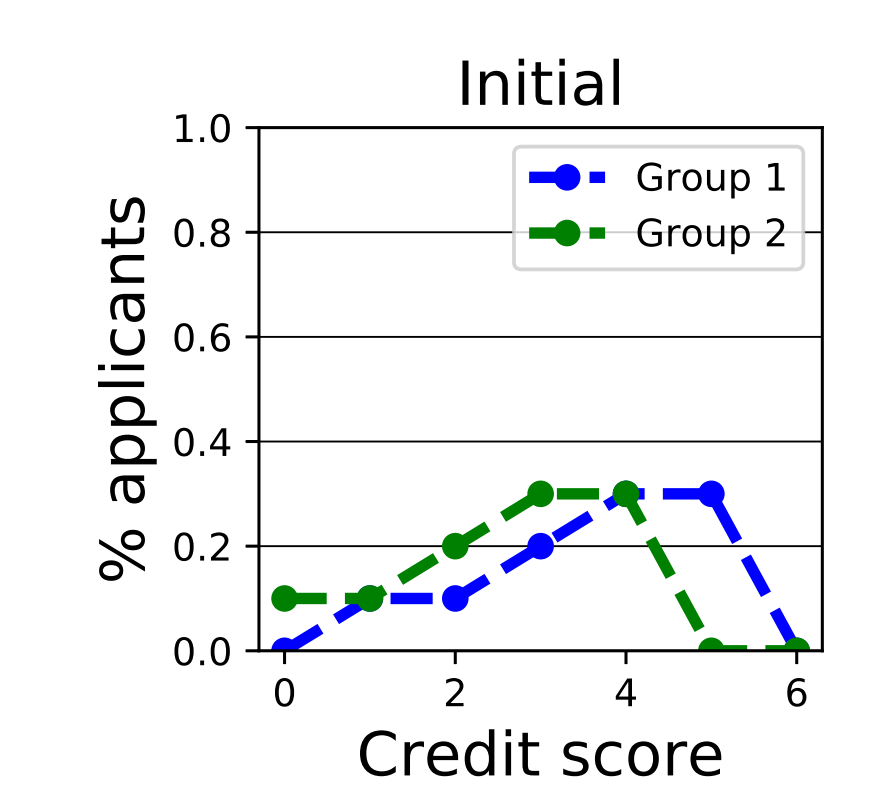
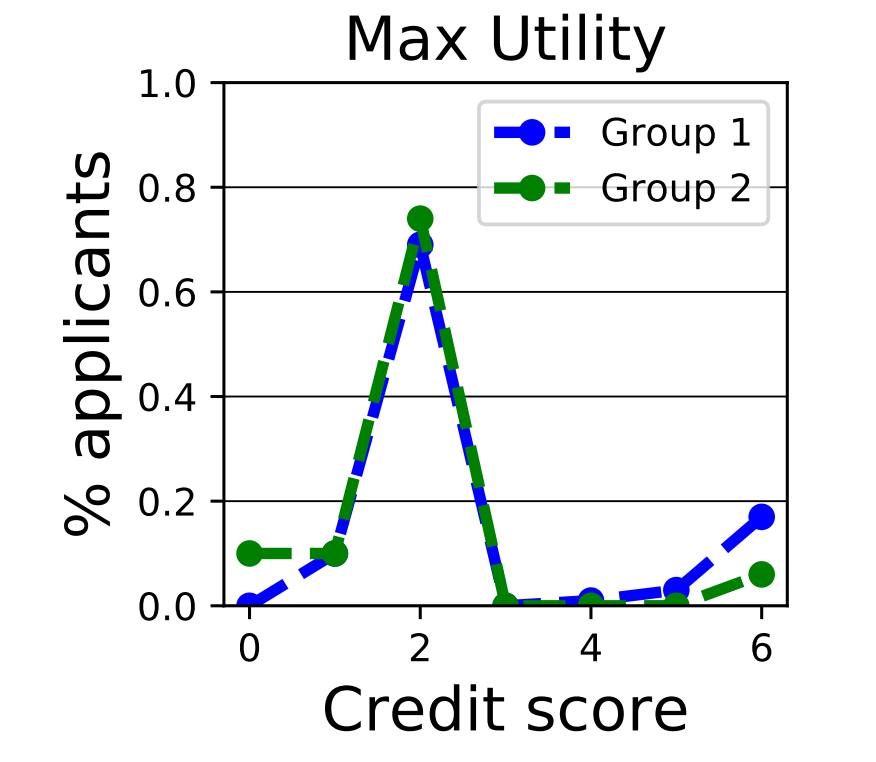
max-reward的方法的结果如下。在论文里有分析，如果经过无穷轮，因为信用一旦低于阈值就永久不再能借款，会导致所有的都到阈值以下。
EO的结果如下：
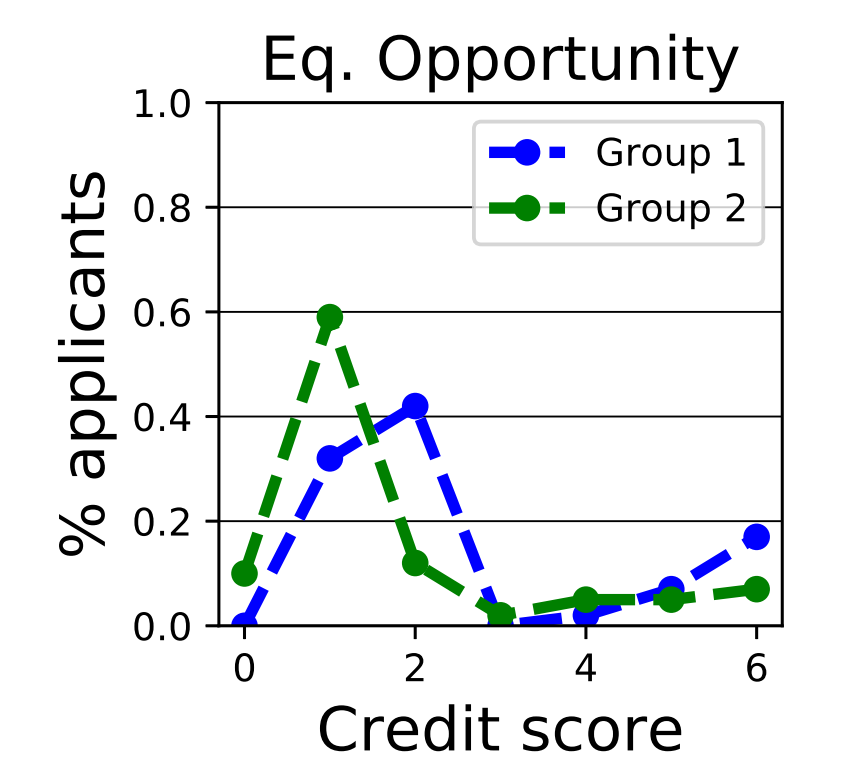
EO相对来说分布的差距还变得更大了。
累计的贷款数量和群体的还款概率如下：
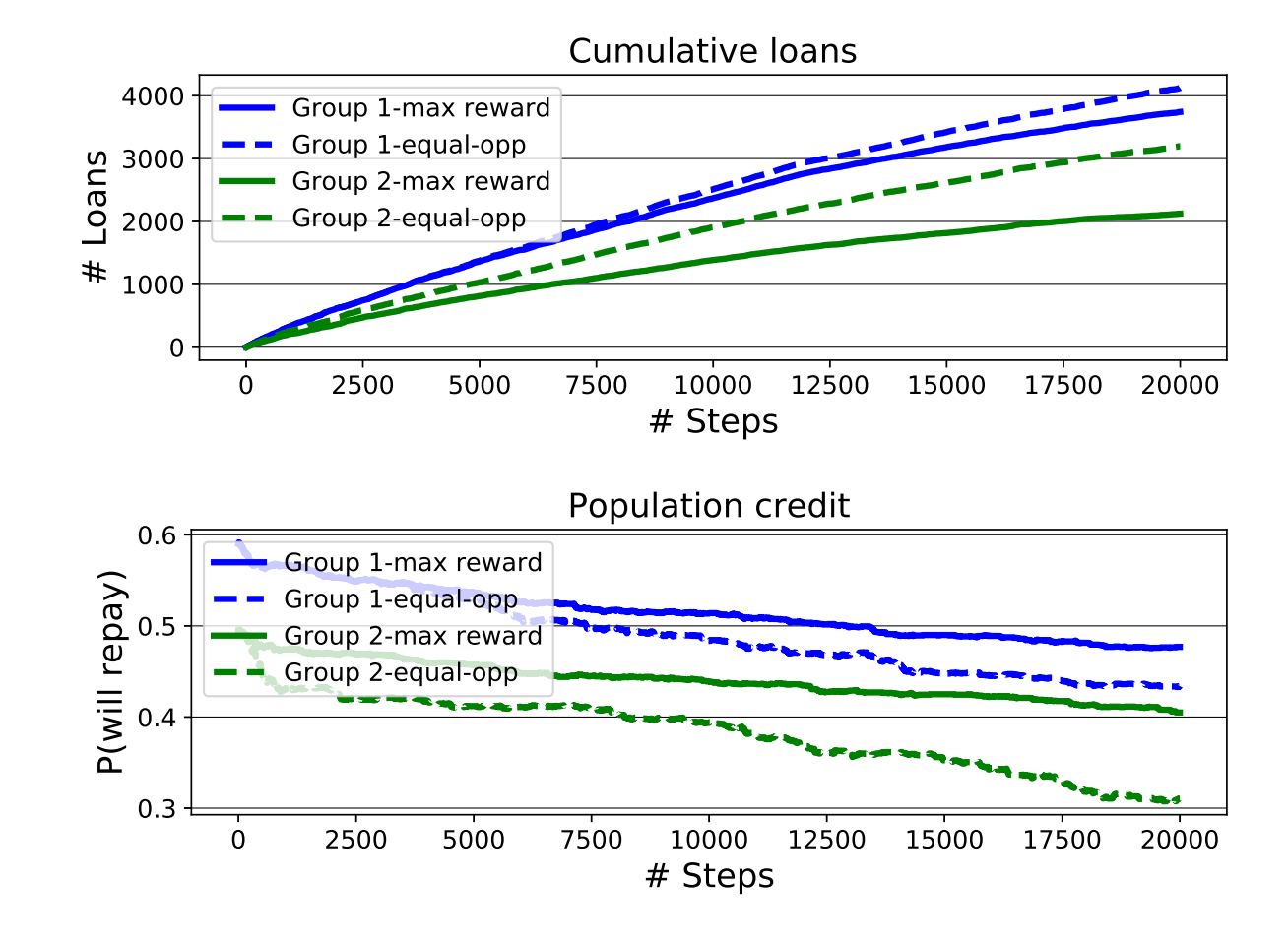
可以看出EO agent会给弱势群体更多的福利，但是群体的信用，弱势群体下降的更快。
下图是EO agent的阈值的设定，和正阳率的一个趋势图。
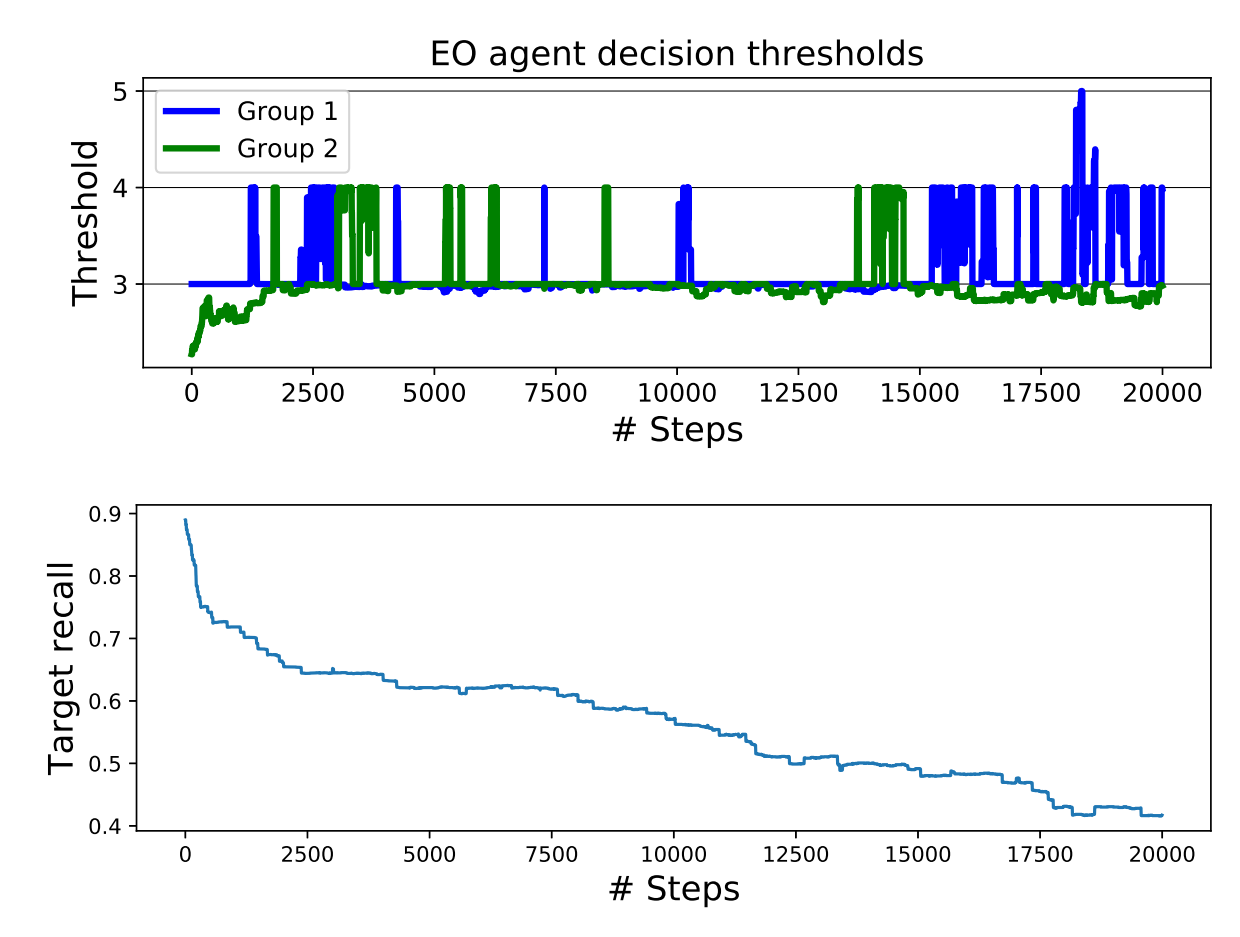
可以看到，对于群体2的阈值设定要更低一点。
而且TPR即使在每一轮中都相同，最后总的TPR也是不同的，如下图。
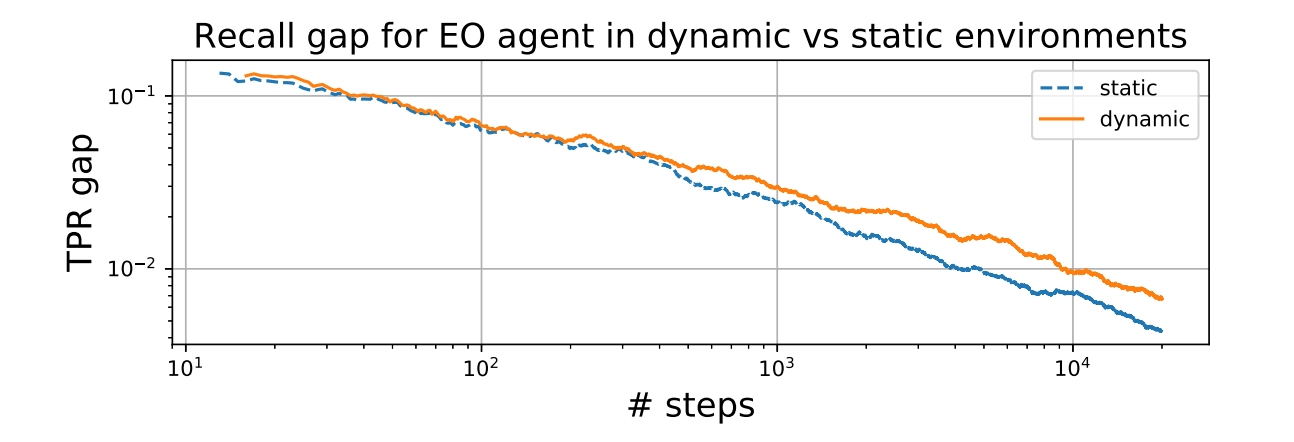
场景二：Attention Allocation
Agent分配有限的注意力到多个不同的地方，每个地方有不同的发生事故的概率，探究不同策略带来的长期影响
Environment：不同地点，每个地点发生事故的数量满足Poisson分布
agent要分配N个注意，有K个地方，每个时间t每个地方发生事故的数目为$y_{kt} \sim \rm{Poisson}(r_k,t)$
发现的数目为$\hat{y}{kt}:=\rm{min}(a{kt},y_{kt})$
考虑动态情况的话，发生的概率会随着attention的数目改变，$d$为常数
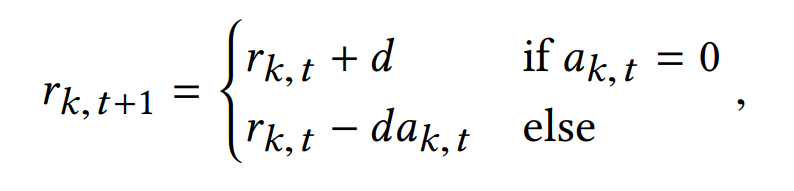
Metrics：
总的发现数目，总的错过数目（真实世界中比较难得到）
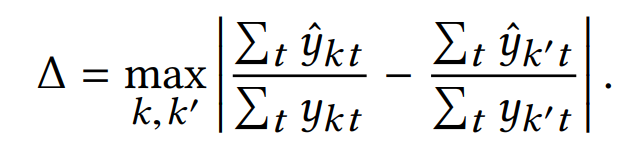
作为公平度量。
Agent：
均匀分配的uniform agent
proportional agents通过对$r$的估计值$\hat{r}$，探索策略epsilon-greedy，$\epsilon$的概率均匀分配，$1-\epsilon$的概率按照原计划
fairness-constrained greedy agent，sequentially的分配，最大化 the probability that the next unit of attention will result in a discovery ， 限制the maximum gap in discovery probabilities between sites小于$\alpha$
实验结果
5地方$[8,6,4,3,1.5]$，6个attention
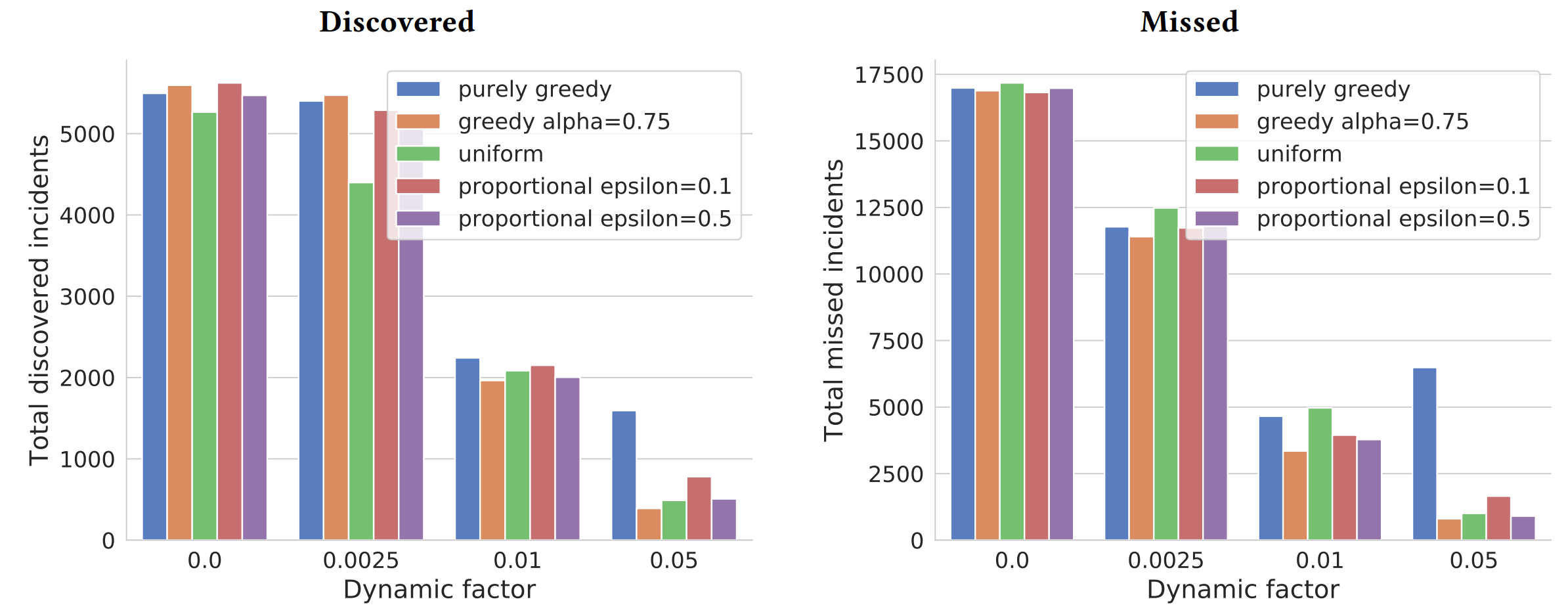
静态环境表现差不多，动态环境中，purely greedy发现高，错过的也高，所以并不能只把发现的作为优化目标。
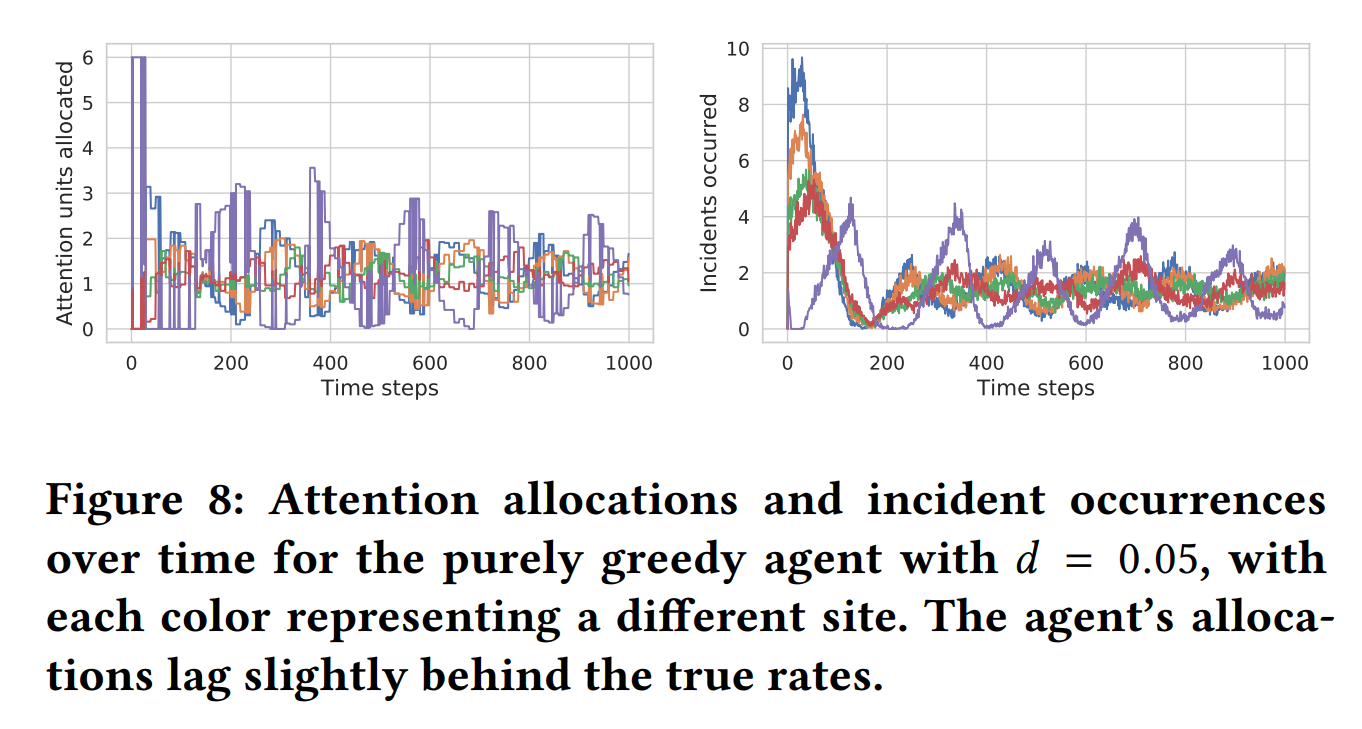purely greedy会过多分配注意在刚刚发现了事故的地方
公平的测量如下
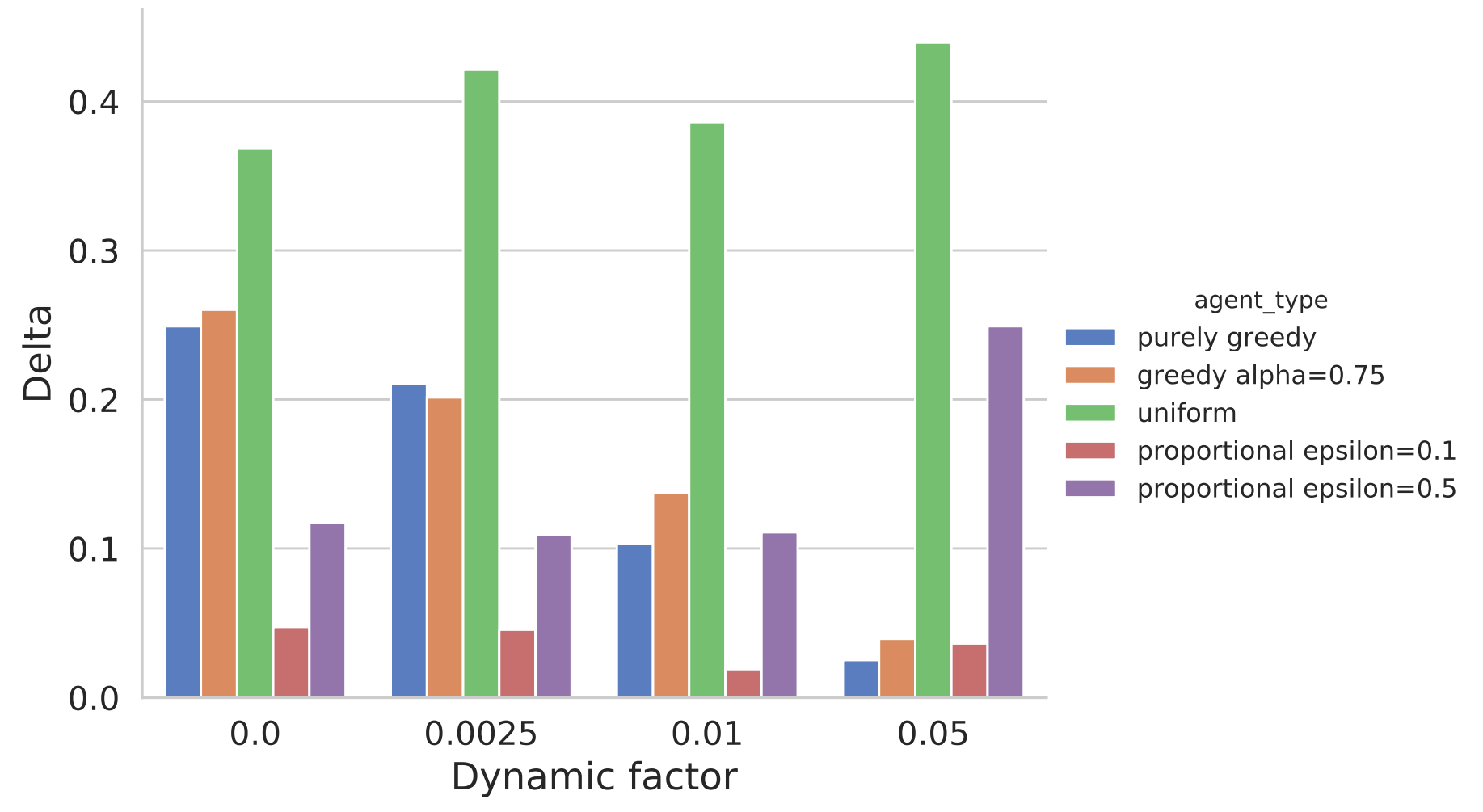
uniform的表现较差，proportional epsilon=0.1和greedy alpha=0.75效果比较好
场景三：college admission
学校要公布选择的规则，申请者可以cost to（可以理解为花费精力）改变分数。是一个Stackleberg博弈。
探索repeated play和以前的one-shot方法达到的均衡的差别。
鲁棒性的策略可能会带来公平问题，合格的人也需要发费精力，而且不同的群体的花费是不同的。
Environment： agent公布阈值分数$\tau$，环境产生带有ground truth的申请者，这些申请者是理性的，只有改分数能去理想的学校而且cost不是过高才会改分数。
Agent：目标是最大化准确度。
static agent前几轮全接受，然后训练一个分类器，使用未更改的(score, label)对，这个label应该是是否合格，但是agent是否知道没说。
robust agent使用以前论文的算法获得一个robust的agent，分类准确率应该是可以达到和未改分情况下一样的准确率。
continuous agent gathers an initial set of unmanipulated applicants, then continuously retrains a non-robust classifier based on the subsequent manipulated scores and labels that it observes.
实验结果
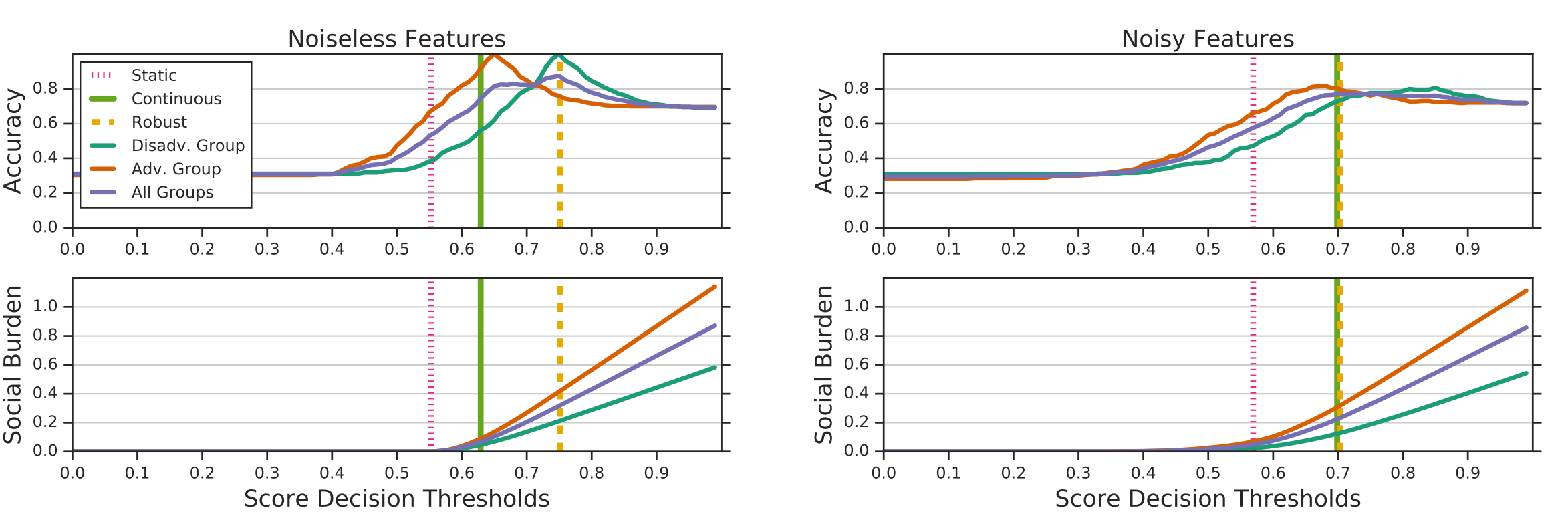
竖着的几条对应着阈值大小
其他的曲线表示阈值与准确率，社会负担（合格者需要的花费）的关系，左边是分数和合格之间的关系没有噪声，右边是有噪声。
可以看到有噪声的情况，即使continuous agent未考虑鲁棒性，结果与鲁棒性agent的结果是一样的。